La sezione aurea ed il numero aureo
La sezione aurea di un segmento Ŕ la parte media proporzionale tra il segmento e la sua parte rimanente
A B : AC = AC : CB AB = s AC = x CB = s-xs : x = x : ( s-x)
risolvendo l’equazione x2 +sx-s2 =0 si ottiene :
x = s (Í 5 - 1 )/2quindi
x /s= ( Í 5 - 1 )/2 = 0,618ma anche x/s=(s-x)/x ossia la parte pi¨ grande Ŕ la sezione aurea di tutto il segmento , mentre la parte pi¨ piccola Ŕ la sezione aurea della pi¨ grande : magia!!
La sezione aurea fu studiata dai Pitagorici i quali scoprirono che il lato del decagono regolare inscritto in una circonferenza di raggio r Ŕ la sezione aurea del raggio e costruirono anche il pentagono regolare intrecciato o stellato, o stella a 5 punte che i Pitagorici chiamarono pentagramma e considerarono simbolo dell’armonia ed assunsero come loro segno di riconoscimento , ottenuto dal decagono regolare congiungendo un vertice si e uno no . A questa figura Ŕ stata attribuita per millenni Ó un’importanza misteriosa probabilmente per la sua proprietÓ di generare la sezione aurea n da cui Ŕ nata
Infatti i suoi lati si intersecano sempre secondo la sezione aurea :
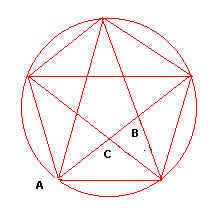
AB : AC = AC : CB
La sezione aurea ha una funzione di grande rilievo nell’espressione della bellezza , per cui fu definita aurea nel Rinascimento.
Il matematico Luca Pacioli (1445-1510) scrisse su di essa un trattato intitolato " De divine proportione " illustrato con figure di Leonardo da Vinci , mostrando sue notevoli applicazioni in campo artistico .Egli sostenne che senza questa proporzione "moltissime cose de admiratione dignissime in philosophia nŔ in alcuna altra scientia mai a luce poteriono pervenire"Il suo entusiasmo per la sezione aurea fu tale da indurlo a metterla in relazione con la DivinitÓ perchŔ anch’essa Ŕ una e trina(3 segmenti sono necessari per la costruzione )


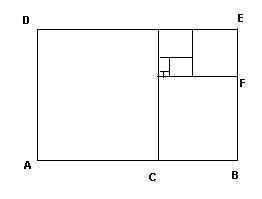
Se disegniamo un rettangolo in cui il rapporto tra l’altezza e la base sia la sezione aurea otteniamo il pi¨ bello , armonico rettangolo tra gli infiniti rettangoli che si possano disegnare e questo spiega la frequenza con cui esso compare in arte
.
AB : AC = AC : CB AC = ADRipetendo la costruzione di un quadrato di lato la sezione aurea dell'altra dimensione del rettangolo si ottengono tanti rettangoli in cui il rapporto tra le due dimensioni Ŕ sempre la sezione aurea
CB=BF
BE : BF = BF : FE
infatti
se AB : AC = AC : CB CB = AB -AC
AB : AC = AC : ( AB-AC) ma anche invertendo antecedenti e conseguenti
AC : AB = ( AB-AC ) : AC applicando la proprietÓ dello scomporre
AC : ( AB-AC) = (AB-AC) : ( AC-CB) quindi siccome AB-AC=BF
AC= BE
CB= BF
AC-CB = BE-BF=FE
quindi BE : BF = BF : FE
Questa costruzione ricorda un’altra caretteristica della sezione aurea: il rapporto tra un numero di Fibonacci f(n) ed il successivo f(n+1) tende al crescere di n alla sezione aurea :
per approfondimenti clicca sull'immagine di Fibonacci
I numeri di Fibonacci : formula ricorsiva per calcolarli : f(n) = f(n-2) +f(n-1)
1 1 2 3 5 8 13 21 34 55 89 144 233
Calcoliamo il rapporto f(n-1)/f(n) e disponiamo i risultati in due colonne
1/1 = 1 1/2= 0,5
2/3 =0,66 3/5= 0,6
5/8= 0,625 8/13= 0,615385
13/21= 0,619048 21/34=0,617684
34/55=0,618182 55/89=0,617978
89/144=0,618056 144/233=0,618026
la prima colonna decresce e la seconda cresce ma entranbe tendono a 0,618033988 che Ŕ il valore della sezione aurea (Í 5 - 1 )/2