 |
Leonardo
Pisano detto Fibonacci (figlio di Bonaccio)(1180-1250)
Fibonacci scrisse il Liber abaci ,libro dell'abaco .In
realtà non tratta dell'abaco ma discute in maniera esauriente metodi e problemi algebrici
, difendendo decisamente l'uso delle cifre indio-arabiche e l'uso dello zero come cifra.Il
padre di Leonardo era un mercante pisano che aveva affari nell'Africa settentrionale e il
figlio ebbe quindi modo di studiare sotto un maestro musulmano e di viaggiare in Egitto ,
in Siria e in Grecia era pertanto naturale che Fibonacci venisse a contatto
con i metodi algebrici arabi , compreso il sistema di notazione
indio-arabico e sfortunatamente in una
forma di espressione retorica il Liber abaci si interessa più dei numeri che della
geometria : esso descrive dapprima le nove figure indiane assieme al segno 0 che in
arabo viene chiamato zefiro da zephirum e dalle sue varianti che sono derivati i nostri
termini di cifra e di zero. |
La sbarretta orizzontale nelle frazioni era
usata regolarmente da Fibonacci ( ed era nota già nota nel mondo arabo ) ma fu solo nel
XVI secolo che entrò nell'uso generale .La sbarretta inclinata fu suggerita nel 1845 dal
matematico A.De Morgan
Il Liber abaci contiene un famoso problema, simile a quello
contenuto nel papiro di Ahmes :Sette vecchie donne andarono a Roma , ciascuna donna
aveva sette muli ,ciascun mulo portava sette sacchi , ciascun sacco conteneva sette forme
di pane e con ciascuna forma di pane v'erano sette coltelli , ciascun coltello era infilato
in sette guaine.
Ma il problema che ispirò i futuri matematici era il
seguente:
Quante coppie di conigli verranno prodotte in un anno a
partire da un'unica coppia se ogni mese ciascuna coppia dà alla luce una nuova coppia che
diventa produttiva a partire dal secondo mese?
Questo famoso problema dà origine alla serie di Fibonacci :
1 1 2
3 5 8 13 21
dove f(n)=f(n-1)+f(n-2)
e che f(n-1)/f(n) tende alla
sezione aurea
Laboratorio
Questo programma in turbo
Pascal calcola il numero aureo
fi soluzione >0 dell'equazione x=1 + 1/x che risulta il limite a
cui tende f(n)/f(n-1)(rapporto tra due numeri di Fibonacci consecutivi) al crescere di n
,ossia l'inverso della sezione aurea di un segmento unitario =2/( Ö5 -1) = (Ö5+1)/2= 1,618
program aureo; (Questo programma calcola il numero aureo )
var n,i: real;
function
fibo(n:real):real;
begin
if (n=1) or (n=2) then fibo:=1
else fibo:=fibo(n-1)+fibo(n-2);
end;
begin
Writeln('Calcolo
dell''approssimazione del numero aureo fi ');
writeln(' soluzione
dell''equazione x= 1+1/x ');
writeln;
writeln('utilizzando i numeri di
Fibonacci f(n) per cui ');
writeln(' f(n+1)/f(n) = fi ');
writeln;
writeln('Inserisci il valore di n
');
readln(n);
i=0;
repeat
i:=i+1;
writeln('f(',i+1:2:0,')/f(',i:2:0,')=
',fibo(i+1)/fibo(i):16:14);
until (i=n);
writeln;
writeln('mentre
il numero aureo fi ottenuto risolvendo l''equazione è');
writeln('fi =
',(1+sqrt(5))/2:2:8);
end.
Questo
programma in Turbo Pascal calcola i quadrati avente per lati i numeri di Fibonacci
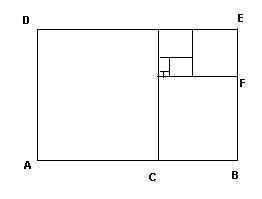
Program fiboquad;
$i graph.p}
var n:integer;
Procedure
quadrato(n:integer);
var k:integer;
begin
for k:=1 to 4 do
begin
forwd(n);
turnright(90);
end;
end;
function
fib(n:integer):integer;
begin
if (n=1) or (n=2)
then fib:=1
else
fib:=fib(n-1)+fib(n-2);
end;
begin
graphcolormode;
showturtle;
turtledelay(100);
setposition(-20,-30);
quadrato(1);
setposition(-21,-30);
quadrato(1);
forwd(1);
n:=3;
repeat
quadrato(fib(n));
forwd(fib(n));
turnright(90);
forwd(fib(n));
n:=n+1;
until n=13;
hideturtle;
end.
