Euclide Elementi X Appendice 27 , vol III p.408-Heiberg                                         

(Nella sua edizione degli Elementi euclidei Heiberg ha collocato questa dimostrazione in appendice come aggiunta spuria , accettando l'ipotesi che si tratti di una dimostrazione nata in ambiente pitagorico.Heiberg la considera un'interpolazione , insieme con tutta l'estrema parte del libro X . Alcuni studiosi avanzano invece l'ipotesi che non si tratti di un'interpolazione , ma proprio di uno spostamento ,che Heiberg esclude: Euclide avrebbe avvertito , alla fine del X libro , l'opportunitā di dimostrare con un esempio l'esistenza di quelle grandezze incommensurabili da lui definite al principio del X libro , e sarebbe ricorso all'esempio classico della diagonale e lato del quadrato .)

Prokeisqw hmiv deixai , oti epi twn tetragwnwn schmatwn asummetroV estin h diametroV thi pleuai mhkei.Estw tetragwnon to ABGD , diametroV de autou h AG legw ,oti h GA asummetroV esti thi AB mhkei .Ei gar dunaton ,estw summetroV: legw oti sumbhsetai ton auton ariqmon artion einai kai perisson...........

Sia da dimostrare che nelle figure quadrate il diametro č incommensurabile col lato in lunghezza.Sia ABCD un quadrato e AC il suo diametro ; dico che AC č incommensurabile in lunghezza con AB .Supponiamo che sia commensurabile : dico che ne conseguirā che lo stesso numero sia insieme pari e dispari.....

Noi oggi diremmo cosė:                         

Il rapporto tra la diagonale ed il lato di un quadrato non sarā mai uguale ad n/m con n ed m interi e primi tra loro.

Per il teorema di Pitagora 2 L2=D2

Se per assurdo D/L =n/m anche D2/L2= n2/m2

e quindi n2/m2=2 ossia  n2=2 m2

ma se 2 č un fattore di n con esponente pari non puō essere contenuto a destra dell'uguaglianza con esponente dispari , quindi il rapporto tra la diagonale ed il lato del quadrato non č un numero razionale (n/m) ma irrazionaleÖ 2= 1,4142..... con infinite cifre decimali

Possiamo dimostrare l'irrazionalitā di Ö 2 con un origami

irr2.bmp (9750 byte)

 

La diagonale del quadrato di lato 12 č 12Ö 2 che č molto vicino a 17

Se Ö 2 fosse un numero razionale , per esempio proprio 17/12 , la diagonale misurerebbe 17 ,  e piegando il lato sulla diagonale resterebbe un triangolo rettangolo isoscele di ipotenusa 7 e cateti 5 , per cui Ö 2 sarebbe anche 7/5 ,mentre un numero razionale ammette un'unica rappresentazione sotto forma di frazione ridotta ai minimi termini,mentre qui 17/12 e 7/5 sono due numeri razionali distinti.

Quindi Ö 2 č un numero irrazionale

 

Costruzione di un segmento di lunghezza Ö n

Partiamo da un triangolo rettangolo isoscele con i cateti di lunghezza unitaria , l'ipotenusa sarā Ö 2 ,facciamo diventare questa ipotenusa il cateto di un nuovo triangolo rettangolo con l'altro cateto nitario, ora l'ipotenusa sarā Ö 3, ora facciamo diventare questa ipotenusa come cateto di un nuovo triangolo rettangolo con l'altro cateto unitario , l'ipotenusa sarā ora Ö 4 ,ecc.

                             chicciola.bmp (128646 byte)

Altra costruzione di un segmento di lunghezza Ö n 

Sia n=a X b

Costruiamo una semicirconferenza di diametro a+b   

 

radicedin.bmp (128646 byte)

Da H tracciamo la perpendicolare ad AB che incontra la semicirconferenza in C

Il segmento CH ha lunghezza Ö n .

Dim   infatti per il II teorema di Euclide  CH2= AH X HB=aXb=n

                                                               CH = Ön

I babilonesi usavano un metodo matematico per calcolare una buona approssimazione

di Ö n

Algoritmo babilonese per il calcolo della radice quadrata di a

Sia a1 una approssimazione per difetto

b1=a/a1 per eccesso

a2=(a1+b1)/2 per eccesso

b2= a/a2 per difetto

a3=(a2+b2)/2

ecc

 

Laboratorio     hacker3.gif (4616 byte)

L'algoritmo babilonese per il suo impianto  iterativo si presta ad essere realizzato mediante un programma in Turbo Pascal :

PROGRAM ALGORITMO;

VAR a,a1,a2,b1,e:real;

BEGIN

CLRSCR;

WRITELN;

WRITELN;

WRITE('PROGRAMMA PER CALCOLARE LA RADICE DI UN NUMERO');

WRITELN;

WRITELN;

WRITELN;

WRITE('INSERISCI IL VALORE DI a ');

READ(a);

WRITELN;

WRITELN;

WRITE('INSERISCI L'' APPROSSIMAZIONE ');

READ(e);

WRITELN;

WRITELN;

REPEAT

WRITE('INSERISCI APPROSSIMAZIONE PER DIFETTO DELLA RADICE DI a ');

READ(a1);

UNTIL (a1*a1<a);

REPEAT

b1:=a/a1;

a2:=(a1+b1)/2;

a1:=a2;

UNTIL (a1*a1-a<e);

WRITELN;

WRITELN;

WRITE('LA RADICE DI a , APPROSSIMATA A MENO DI ',e:10:8,' E'' ', a1:10:8);

WRITELN;

WRITELN;

END.

La radice cubica di 2

Il Problema di Delo

Delo č un'isola dell'arcipelago greco, patria di Apollo.Durante una pestilenza ad Atene , gli abitanti mandarono un emissario a chiedere all'oracolo di Apollo a Delo cosa fare.L'oracolo rispose che la pestilenza sarebbe cessata non appena gli Ateniesi avessero raddoppiato la grandezza dell'altare di Apollo.

La pestilenza non cessō perchč gli Ateniesi non seppero costruire ,con riga e compassa , unici strumenti che possedevano,un cubo di lato la radice cubica di 2 , per raddoppiare un cubo di lato 1

Oggi sappiamo che non č possibile .

Le regole di Euclide  non prevedono di  fare segni sulla riga , ma se si mettono due segni X e Y a distanza 1 sulla riga , con la costruzione della figura  

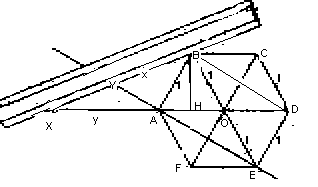
delo.bmp (7542 byte)

  si costruisce un segmento YB di lunghezza radice cubica di 2

XY : YB = y:2

1:x=y:2

xy=2      (*)

dim:

BH =Ö 3/2  

AH =1/2  XH=y+1/2     XB=1+x      

    XB2 = XH2 + BH2

    (1+x)2=(y+1/2)2+(Ö3/2)2

  1+x2+2x=y2+1/4 +y+3/4

  x2+2x=y2+y          posto y=x2      che soddisfa (*)

  y+2x=y2 +y

  2x=x4

  x3=2

  x=radice cubica di 2     e y= radice cubica di 4  che verifica  xy=2

Altra costruzione per la radice cubica di 2:

Mediante le coniche :

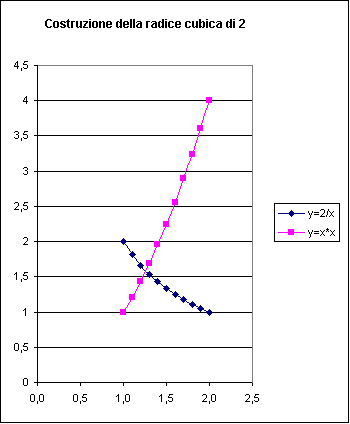
mettendo a sistema l' iperbole xy=2 con la parabola y=x2

il punto di intersezione ha come ascissa la radice cubica di 2:

dim

xy=2

y=x2         

 

y=2/x

2/x=x2

x3   = 2     x=radice cubica di 2

    

x y=2/x y=x*x
1,0 2 1
1,1 1,818182 1,21
1,2 1,666667 1,44
1,3 1,538462 1,69
1,4 1,428571 1,96
1,5 1,333333 2,25
1,6 1,25 2,56
1,7 1,176471 2,89
1,8 1,111111 3,24
1,9 1,052632 3,61
2,0 1 4