
Questo lavoro è stato proposto nell'a.s.2000/2001 agli alunni della 1° e 2° A del Liceo Ginnasio Vittorio Emanuele II di Napoli come pretesto per approfondire e nello stesso tempo rendere più gradevole il discorso sui numeri .Gli alunni hanno risposto con entusiasmo e con ottimi risultati !!
Molti argomenti di questo lavoro possono diventare exibit di matematica da presentare durante manifestazioni di fine anno, come quella che si tiene ogni anno nella mia scuola : il Vittorio Emanuele Day , o in occasioni simili.
Ogni sezione è corredata da attività di laboratorio informatico
Questa mia esperienza è stata da me illustrata durante il Convegno Hermes "La rete nella didattica - la didattica nella rete "
Alcuni strani numeri ( con 120 cifre decimali!!!):

1 3 6 10 15 21 ...
I numeri triangolari si ottengono sommando 1+2+3+4+5+....
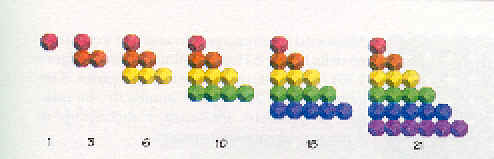
T(n)= 1+2+3+...+n ed anche T(n) = T(n-1)+n
Il doppio di un numero triangolare è pari al rettangolo di lati n e n+1

2T(n) = n(n+1) o anche T(n)=1/2 n(n+1) infatti :
dim per induzione
il teorema vale per n=1 , supponiamo che valga per n-1 ossia che T(n-1) = 1/2 (n-1)n e dimostriamo che vale anche per n:
T(n)=1/2(n-1)n +n = n(1/2 n-1/2 +1) = n(1/2 n +1/2) = 1/2 n(n+1)
La somma di due numeri triangolari consecutivi T(n-1) + T(n) è uguale al numero quadrato n2
T(n-1) + T(n) = n2
dim:
T(n-1) + T(n) = T(n-1) + n+ T(n-1) = n+ 2 T(n-1)= n + 2 X 1/2 n (n-1) = n2
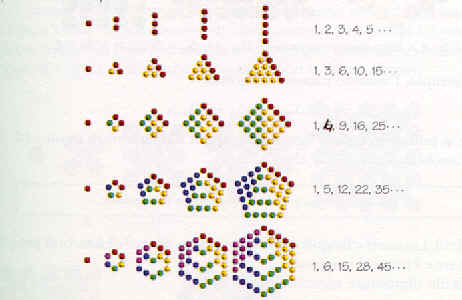
I vari tipi di numeri poligonali si ottengono sommando i primi n termini di opportune progressioni aritmetiche che partono da 1:
1+1+1+1+1.... (ragione d=0) numeri naturali 1 2 3 4 5.....
1+2+3+4+.... (ragione d=1) numeri triangolari 1 3 6 10 15...
1+3+5+7+... (ragione d=2) numeri quadrati 1 4 9 16 25 ...
1+4+7+10+13+ (ragione d=3) numeri pentagonali 1 5 12 22 35...
1+5+9+13+17+ (ragione d=4) numeri esagonali 1 6 15 28 45....
1+6+11+16+21+. (ragione d=5) numeri ettagonali 1 7 18 34 55...
1+7+13+19+25+. (ragione d=6) numeri ottagonali 1 8 21 40 65...

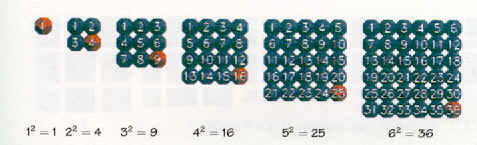
I numeri quadrati perfetti
Ogni numero esagonale è triangolare ed è un rettangolo nX(2n-1)
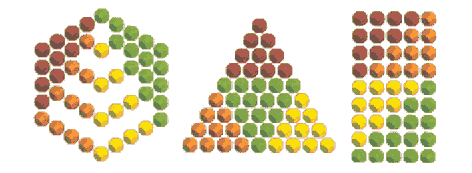
Se la base delle piramidi è un triangolo (numeri tetraedrici P3(n))
1 4 10 20 ....

Si ottengono sovrapponendo i numeri triangolari
6 copie di un numero tetraedrico P3(n) sono contenute in una scatola di dimensioni n X (n+1) X (n+2)
ossia P3(n) =1/6 n(n+1)(n+2)
Se la base della piramide è un quadrato (numero piramidale quadrato P4(n))
Si ottengono sovrapponendo i numeri quadrati

6 copie di un numero piramidale quadrato P4(n) formano un parallelepipedo di dimensioni n X (n +1) X (2n+1)
e 3 copie di un numero piramidale quadratoP4(n) coprono il rettangolo di dimensioni
(2n+1) X T(n)= (2n+1) X 1/2 n (n+1)= 1/2 n(n+1)(2n+1) e quindi
P4(n) = 1/6 n(n+1)(2n+1)
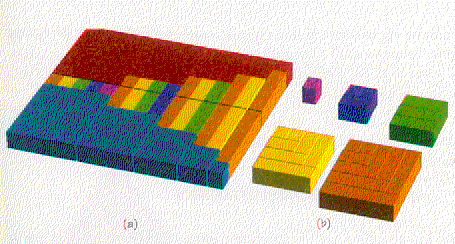
Possiamo costruire una piramide costruita con i cubi :
Pcubo(n)= 13 + 2 3 + 3 3 + 43 + 53......
e dimostrare che il numero piramidale a 4 dimensioni è uguale al quadrato del numero triangolare T(n)
Pcubo(n)=T(n)2=1/4 n2(n+1)2

Per definizione 0! =1
1! = 1
2! = 1 X 2
3! = 1 X 2 X 3 = 6
4! = 1 X 2 X 3 X 4 = 24
ecc. n! = n (n-1)!
Laboratorio 
Questo programma calcola il fattoriale di un numero n
Vuoi lanciare il programma ? Clicca
qui
![]()
PROGRAM FATTORIALE;
VAR
N:real;
BEGIN
IF( N=0) OR (N=1) THEN FATT:=1
ELSE FATT:= FATT(N-1)*N;
END;
BEGIN
WRITELN('INSERISCI
IL NUMERO DI CUI VUOI IL FATTORIALE ');
READLN(N);
WRITELN('IL
FATTORIALE DI ', N:8:0 , ' E'' ', FATT(N):16:0);
END.
A differenza dei numeri di Fibonacci , i numeri di Padovan cominciano con il numero 1 ripetuto 3 volte , mentre la regola di costruzione è
P(n) = P(n-3)+ P(n-2)
1 1 1 2 2 3 4 5 7 .....
Laboratorio 
Questo programma in Turbo Pascal calcola i primi n numeri di Padovan
Clicca qui per lanciare
padovan.com
![]()
program
padovan;
var
n,k:integer;
function
pado(n:integer):integer;
begin
if (( n=1 ) or (n=2)) or (n=3) then pado :=1
else pado:=pado(n-3)+pado(n-2);
end;
begin
clrscr;
writeln('quanti numeri di Padovan
vuoi?');
readln(n);
for k:=1
to n do
writeln(pado(k):12:0);
end.
Il numero di plastica è la soluzione dell'equazione x= 1/x + 1/x2
ma anche il valore a cui tende la successione dei rapporti P(n+1)/P(n)
Laboratorio 
Questo programma in Turbo Pascal calcola il rapporto di P(n+1)/P(n) e lo confronta con il numero di plastica, si ottiene una buona approssimazione del numero di plastica già per n=30.
Clicca qui per lanciare plastica.com
![]()
program plastica;
var n:integer;
function pado(n:integer):integer;
begin
if ((n=1) or (n=2)) or (n=3) then pado:=1
else pado:=pado(n-2)+pado(n-3);
end;
begin
clrscr;
writeln('Calcolo dell''approssimazione ');
writeln(' del numero di plastica p ');
writeln('soluzione dell''equazione x=1/x+1/x^2 ');
writeln(' come rapporto tra due successivi ');
writeln('numeri di Padovan p(n+1)/p(n) ');
writeln('quale numero vuoi inserire ? ');
readln(n);
writeln('p(',n+1,')/p(',n,')= ',pado(n+1)/pado(n):2:12);
writeln('mentre il numero di plastica calcolato come ');
writeln(' soluzione dell''equazione è p = 1,324718 ');
end.
Un numero è primo quando è divisibile solo per se stesso e l'unità
Eratostene (276-194 a.C. ) bibliotecario della grande biblioteca di Alessandria elaborò un metodo per l'individuazione dei numeri primi , detto crivello di Eratostene (setaccio) eccolo:
Si scrivono i numeri in successione 1 2 3 4 5 6 7 8 9 10 ......
Partiamo da 1 segniamo con un cerchietto il 2,
cancelliamo un numero ogni 2 dal 2 in avanti
facciamo un cerchietto intorno al numero successivo ,ossia 3
cancelliamo un numero ogni 3 dal 3 in avanti
facciamo un cerchietto intorno al numero successivo ossia 5
cancelliamo un numero ogni 5 ecc..
Così facendo, nei cerchietti restano solo i numeri primi
Si dicono perfetti i numeri somma dei fattori del numero stesso :
6 = 1+2+3 dove 1 , 2 e 3 sono i fattori di 6
28 = 1+2+4+7+14 dove 1,2,4,7 e 14 sono i fattori di 28
Una terna di interi a,b,c formano una terna di numeri pitagorici se :
a2 + b2 = c2
Se a,b,c non hanno fattori comuni , la terna è detta primitiva.
Tutte le terne pitagoriche si ottengono da :
a = v2 - u2
T) b = 2uvc = u2 + v2
con u e v interi primi tra loro e non entrambi dispari, v>u
Dim:
Posto a/c=x e b/c = y segue x2+ y2=1
y2=(1-x)(1+x)
y/(1+x)=(1-x)/y posto = t = u/v segue
tx - y = -t
x + ty = 1 che risolto dà
x = (1-t2)/(1+t2)
y = 2t/(1+t2)
Sostituendo x,y,t si ottiene :
a/c = (v2-u2)/(u2+v2)
b/c = 2uv/(u2+v2) da cui
a = (v2-u2) r
b = 2uv r
c = (u2+v2) r con r fattore di proporzionalità quindi per r =1
vale l'enunciato T)
Per definizione è il rapporto tra la lunghezza della circonferenza e il diametro
di conseguenza anche : la lunghezza di una circonferenza di diametro 1,oppure l'area di un cerchio di raggio 1.
Fin dai Babilonesi si è tentato di calcolare un valore approssimato di p
Archimede ottenne un'approssimazione di p calcolando l'area di un poligono di 96 lati, inscritto in un cerchio di raggio 1
(Inizio del Trattato "Misura del Cerchio"nell'edizione di Basilea dell'opera di Archimede(1544)

L'astronomo cinese Tsu Ch'ung chih (nato nel 430 d.C.) aveva trovato come approssimazione 22/7 ed una più accurata 355/113; il grande matematico indiano Brahmagupta(600 d.C.) aveva calcolato come approssimazione di p la radice di 10
Nel 1593 Vieta esibì una formula di p
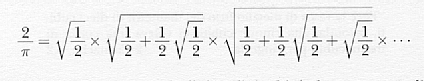
partendo dalla considerazione che la successione numerica delle aree dei poligoni di 4 ,8,16 ecc.. lati inscritti in un cerchio di raggio 1 tende a p
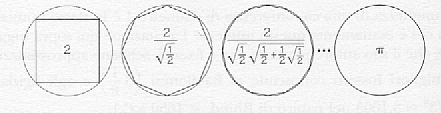
Alla fine del 1500 in Germania Ludolph van Ceulen, che aveva passato gran parte della sua vita nel calcolo di p, calcolò 20 cifre decimali di p.
Il tedesco Lambert nel 1761 dimostrò che p non è un numero razionale e Lindemann nel 1882 che p non è soluzione di nessuna equazione algebrica con coefficienti interi
Costruzione di un segmento lungo p
.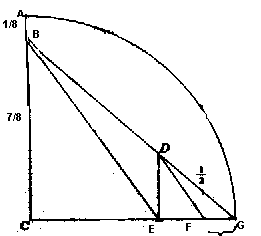
Nel quadrante di raggio unitario costruire
AB =1/8 BC=7/8 DG=1/2
Con facili calcoli (..BG= Ö113/8 , DE=7Ö113/226, EG=4Ö113/113, CE=(113-4Ö113)/113, EF=(28Ö113-112)/791) si arriva a :
FG = 16/113 = 0,1415929....e siccome
355/113 = 3+16/113 =3,1415929...
che è un'approssimazione di p a meno di un milionesimo,
per costruire un segmento che approssimi p, basta aggiungere un segmento lungo 3 al segmento FG
Un'approssimazione statistica di p
Calcoliamo la probabilità di colpire la parte interna di un cerchio di raggio r inscritto in un quadrato: prob = n. eventi favorevoli/n. eventi possibili = p r2/4 r2= p /4
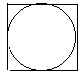
prob = p/4 p = prob X 4 dopo aver ottenuto per via sperimentale la probabilità di colpire la parte interna del cerchio inscritto nel quadrato (10000 ,20000 tiri ), oppure mediante una simulazione al computer ,per cui prob = 0.785398... di conseguenza
p = 0.785398... X 4 = 3.141592....
Laboratorio 
Questo programma simula il lancio di un certo numero di proiettili verso un bersaglio costituito da un cerchio inscritto in un quadrato e calcola la frequenza dei tiri che colpiscono il bersaglio e da questa un valore approssimanto di p
Clicca qui per lanciare
pgreco.com
![]()
program
pgreco;
var
x,y,freq,n,i:real;
writeln('quanti tiri vuoi fare?');
readln(n);
freq:=0;
i:=0;
repeat
i:=i+1;
x:=random;
y:=random;
if(
(x*x+y*y)<1) then freq:=freq+1;
until
(n=i);
writeln('su ',n:10:0,' tiri ne sono
arrivati sul bersaglio ',freq:10:0);
writeln('la frequenza di colpire
l''interno di un cerchio inscritto');
writeln(' in un quadrato è
',freq/n:10:8);
writeln(' di conseguenza un valore
statistico di p greco è ', freq*4/n:10:8);
end.
Questo programma simula anche graficamente il tirassegno
Clicca qui per lanciare
pdisegno.com
![]()
program pdisegno;
{$i graph.p}
var
j,x,y:integer;
i,n, k:real;
graphcolormode;
setposition(0,0);
for j :=1
to 4 do
begin
forwd(90);
turnright(90);
end;
arc(250,100,-90,90,1);
k:=0;
writeln('quanti tiri vuoi fare? ');
readln(n);
i:=0;
repeat
i:=i+1;
x:=160+trunc(random*90);
y:=100-trunc(random*90);
if (((x-160)*(x-160)+(y-100)*(y-100))<8100) then
begin
plot(x,y,2);
k:=k+1;
end
else plot(x,y,1);
until
(i=n);
for j:=1
to 13 do
writeln;
writeln('la parte interna all''arco
e'' ');
writeln(' stata colpita',k:8:0, '
volte');
writeln('il calcolo approssimato
per');
writeln('via statistica di p greco
e''' , k*4/n:10:8);
end.
Consideriamo le due progressioni numeriche per es. :
0 1 2 3 4 5 6 7
1 3 9 27 81 243 729 2187
Il prodotto di due termini della progressione geometrica appartiene ancora alla progressione
e dista dall'unità quanto la somma delle distanze dei due fattori
(es. 9X243 = 2187 2+5 = 7 ) (i numeri in rosso sono i log dei numeri neri in base 3 )
Queste osservazioni furono fatte da Archimede ma riprese da Stifel (1544) che costruì una prima tavola dei logaritmi in base 2
Ma solo Burgi e Napier (Nepero) riuscirono a costruire tavole dei logaritmi organiche anzi Burgi un po' prima di Nepero ma quest'ultimo le pubblicò per primo(nel 1614).
Consideriamo
0 k 2k 3k ...... nk (1)
1 (1+k) (1+k)2 (1+k)3 (1+k)n (2)
ponendo a=(1+k)n e b= nk
a=(1+k)b/k = ((1+k)1/k))b
quindi b è il logaritmo di a in base (1+k)1/k
ossia i termini della progressione aritmetica (1) sono i logaritmi dei relativi termini della progressione geometrica (2) nella base (1+k)1/k
Ora quanto più piccolo è k tanto più piccola sarà la differenza tra due termini della (1) e migliore sarà il sistema di calcolo dei logaritmi per cui la base migliore è quella per cui k->0 (1/k=n tendente all'infinito ) ossia lim (1+1/n)n=e
Compare così il numero di Nepero e anche se esso resta indissolubilmente legato al nome di Eulero ( che fu il primo a chiamarlo e)il quale definisce e come somma della serie 1 + 1/1! +1/2! + 1/3! + ......+1/n! + ...
Nepero scelse k= 1/107 e preferì utilizzare come base (1- 1/107 )10^7=0,999999910^7
Per evitare cifre decimali moltiplicò il numero per 107
ossia N=107(1-1/107)L dove L è il logaritmo neperiano di N per cui
il logaritmo di 107 è 0
il logaritmo di 9999999 è1 si vede subito che tale logaritmo non è quello che oggi chiamiamo neperiano ,ossia in base e, infatti
log N(in base e) = log107+ L log (1-1/107) con L =logaritmo di Nepero
quindi L = (log N -log 107 )/ log (1-1/107)
Nel 1615 Briggs fece visita a Nepero e gli propose di costruire una tavola di logaritmi in base 10 , ma dovette portare da solo a termine il progetto per la sopraggiunta morte di Nepero nel 1617
Egli risolse il problema utilizzando estrazioni di radici successive
es . \/¯10 = 3,162277 quindi log 3,162277 =0,5
10 3/4 = \/¯(10 \/¯10) = \/¯( 10 X 3,162277) = \/¯31,62277=5,62341 quindi log 5,62341=3/4 =0,75 ecc...
Briggs nell'anno della morte di Nepero pubblicò la tavola dei logaritmi in base 10 da 1 a 1000
Anche Burgi aveva costruito delle tavole di logaritmi ma era partito da (1+1/104)10^4 ed aveva moltiplicato il numero per 108 ossia N=108(1+1/104)L con L =logaritmo di N
Laboratorio 
Questo programma calcola un'approssimazione di e come limite per n tendente all'infinito della successione (1+1/n)n
Clicca qui per lanciare numeroe.com
![]()
program nepero;
var comodo,e:real;
risposta :char;
i,n:integer;
begin
writeln('QUESTO PROGRAMMA CALCOLA UN
VALORE APPROSSIMATO DI e');
repeat
e:=1;
writeln('introduci il valore di n ');
readln(n);
comodo:=1+1/n;
for i:=1 to n do
e:=comodo*e;
writeln('il valore di e = ',e);
writeln('vuoi un nuovo valore di e?
');
readln(risposta);
until (risposta='N') or
(risposta='n');
end.
Questo programma calcola un'approssimazione di e utilizzando la formula:
e= 1 + 1/1! + 1/2! + 1/3! + .....+1/n!+....
Clicca qui per lanciare nepero2.com
![]()
program nepero2;
var e:real;
i,fatt,n:integer;
risposta:char;
begin
repeat
e:=1;
fatt:=1;
writeln('inserisci n');
readln(n);
for i:=1 to n do
begin
fatt:=fatt*i;
e:=e+1/fatt;
end;
writeln('il
valore di e = ', e);
writeln('vuoi
continuare?');
readln(risposta);
until
(risposta='N') or (risposta='n');
end.
Per definizione i=Ö -1
Le potenze di i :
i =Ö -1
i2=-1
i3=-i
i4=+1
i5=i ecc. le potenze si ripetono ciclicamente