Consideriamo due serie numeriche, una rappresentante i logaritmi e una i numeri, contenenti entrambe il parametro K

0             k               2k               3k          ......     nk             (1)

1        (1+k)         (1+k) 2          (1+k) 3    ......    (1+k) n         (2)

Ponendo a come una potenza n di 1+k e b come nk [ a=(1+k) n     e     b= nk ] allora a sarà uguale ad 1+k elevato a b/k [a=(1+k) b/k ] che a sua volta è uguale a ((1+k) 1/k )) b . Dato che in precedenza abbiamo considerato le 2 serie numeriche, la prima costituente i logaritmi e la 2 i numeri, in questa forma possiamo definire b come logaritmo di a. Se definiamo logaritmo l'esponente cui deve essere elevata una base per ottenere un numero b è il logaritmo di a. si deduce quindi che per la costruzione di una tabella di logaritmi di valori molto vicini tra loro bisogna porre il parametro k più vicino allo 0.

k -> 0

1/k = n tendente ad infinito

Il limite di n >infinito di (1+1/n)n è uguale ad e. Di conseguenza e non è altro che la base più comoda per creare una tabella di logaritmi contenente il maggior numero di valori quanto più vicini tra loro.

.

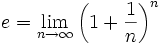Essa può anche essere espressa in molti modi mediante serie infinite ; la più importante di queste espressioni è
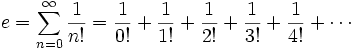