I FRATTALI : LE NUOVE FRONTIERE DELLA GEOMETRIA
Oriana Pagliarone
Se ti piacciono i frattali è perché tu stesso sei fatto di frattali.
Se non li sopporti, non sopporti te stesso.
Capita.
(Homer Smith,ingegnere informatico di Art Matrix)
Introduzione alla geometria dei frattali
Una decina di anni fa Benoît Mandelbrot ha descritto in termini grafici forme e processi naturali, rappresentando oggetti dai contorni molto frastagliatie complessi, attraverso rigorosi metodi matematici.
Nasceva quella branca della Matematica che Mandelbrot ha chiamato Geometria dei Frattali.
Essa è capace di rappresentare i profili di una montagna o di una costa , le nuvole, le strutture cristalline e molecolari, e addirittura le galassie.
La parola "frattale" definisce una rappresentazione grafica composta di linee spezzate (da latino fractus) dall'andamento apparentemente irregolare, che sono in sostanza delle strutture matematiche, capaci di esprimere comportamenti variabili in spazi anche molto piccoli.
Inoltre i frattali hanno sempre una dimensione fratta , non intera.
Essi sono forme geometriche le cui parti, anche minime, contengono un'infinita ricchezza di dettagli.
Con i frattali si costruiscono modelli matematici semplici di oggetti complessi, come spugne, fiocchi di neve, foreste.
Vi sono molti tipi di frattali, ma tutti hanno una cosa in comune: generano forme spaziali complesse da regole semplici.
Ogni dettaglio del frattale riproduce la forma del tutto (proprietà di autosomiglianza). Il termine usato da Mandelbrot è self-similarity.
Benoit Mandelbrot
E' nato a Varsavia nel 1924 ed ha studiato all'Ecole Politecniche di Parigi, al California Institute of Technology e all'Università di Parigi, dove si è laureato in matematica. Nel 1958 ha iniziato la collaborazione con l'IBM; oggi è professore di matematica alla Harvard University.Tra i numerosi riconoscimenti che gli sono stati assegnati, spicca la F.Barnard Medal della National Accademy of Sciences della Columbia University. La più completa esposizione della sua ricerca è racchiusa nel volume "The fractal geometry of nature"(S.Francisco 1982).
Proprietà dei frattali
Autosomiglianza : ogni dettaglio di un frattale riproduce la forma del tutto
Dimensione fratta: la curva di Koch ha dimensione 1.26
la sbarra di Cantor ha dimensione 0.63
Dimensione di un oggetto
Per la geometria euclidea un punto ha dimensione 0, una retta ha dimensione 1, un piano ha dimensione 2, un cubo ha dimensione 3.
Ma è proprio sicuro che la dimensione di un oggetto sia univocamente determinato?
Proviamo a ripetere il ragionamento che fa Mandelbrot per avvicinarci ad una amplificazione del concetto di dimensione. Facciamo un esempio prendendo in considerazione un gomitolo di lana, di 10 cm di diametro, fatto con un filo di 1 mm di diametro. Con un grado di risoluzione di 10 m il gomitolo è un punto e ha quindi dimensione 0, con una risoluzione di 10 cm è una palla con dimensione 3, ma con una risoluzione di 10 mm torna ad essere un insieme di fili quindi di dimensione 1 e se arriviamo a una risoluzione di 0,1 mm i fili diventano dei cilindri tridimensionali.
Con una risoluzione di 0,01 mm ogni cilindro torna ad essere formato da fibre filiformi e la dimensione torna ad essere 1 e riducendo ancora la risoluzione si arriva agli atomi di dimensione 0. E allora qual è la dimensione di un gomitolo di lana?
Per rispondere a questa domanda occorre prima stabilire il modello geometrico da utilizzare e stabilire la risoluzione più adeguata al contesto in cui ci troviamo e quindi la dimensione di un oggetto dipende dal rapporto tra oggetto ed osservatore.
Dopo aver scardinato questo primo assioma, ossia che la dimensione di un oggetto sia univocamente determinata, diamo uno scossone ad un altro concetto: che la dimensione degli oggetti sia sempre un intero.
Ci sono oggetti, i frattali appunto, che non hanno dimensione intera bensì frazionaria.
Per capire questa affermazione occorre avvicinarci alla formula per il calcolo della dimensione sviluppata da Hausdorff (1919) che usa il concetto di ricoprimento, di omotetia e di rapporto di omotetia.
Verifichiamo la validità della formula della dimensione secondo Hausdorff:
Dimensione secondo Hausdorff : D = log N/ log(1/r)
D = dimensione
N = numero di ricoprimenti
r = rapporto di similitudine
Consideriamo un segmento AB
![]()
Dividiamolo in 2 parti ( r = 1/2 ) A B
N = numero di ricoprimenti = 2
D = dimensione = 1
Siccome 21 = 2 si deduce che
(1/r)D = N e passando al logaritmo
 Consideriamo
un quadrato
Consideriamo
un quadrato
Dividiamo ogni lato in due parti (r =1/2)
Costruiamo i 4 quadrati che ricoprono il quadrato di partenza N= numero di ricoprimenti = 4 D = dimensione = 2
Siccome 22=4 si deduce che
(1/r)D = N e passando al logaritmo
log (1/r)D = log N ossia
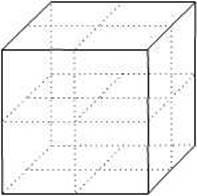
Consideriamo un cubo di lato l
Dividiamo ogni lato in 2 parti (r = ½ )
Otteniamo così 8 cubi
D = 3
N = 8
23 = 8
(1/r)D= N
D = log N/ log(1/r) = log8/log2 = 3log2/log2 = 3
Galleria di frattali
La curva di Koch
Ora avviciniamoci ad un oggetto frattale molto famoso: la curva di Koch (fig.1)
Nel 1905, il matematico svedese Helge von Koch descrisse una struttura che ricorda un fiocco di neve, dai bordi frastagliati e dalle forme simmetriche. Per chi mastica un po’ di matematica è una curva continua ma non derivabile, dalle proprietà particolari: autosomiglianza, dimensione fratta, perimetro che tende all’infinito, area però limitata.
Analizziamole nel dettaglio:
Autosomiglianza della curva di Koch
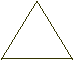
La curva di Koch è costruita partendo da un triangolo equilatero .
Si divide il lato in tre parti uguali e su ogni lato, nella parte centrale, si disegna un
nuovo triangolo equilatero di lato l/3. Si ripete il procedimento su ogni segmento
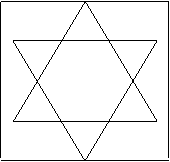
Ad ogni passo il contorno diventa più frastagliato (fig.1)
Dimensione della curva di Koch
(1/r)D = N N = 4 r = 1/3
D = log N/log(1/r)
D = log 4/log 3 = 1.26
Perimetro della curva di Koch

P0 = 3· l
P1= 3·l·(4/3)1

P2= 3·l·(4/3)2
Pn= 3·l·(4/3)n
lim Pn = ∞
n ->∞
Ossia il perimetro della curva di Koch tende all’infinito
Area della curva di Koch
La curva di Koch è sempre contenuta nel quadrato di lato 2·√3·l /3
Sn < 4l2/3
Polvere di Cantor
La polvere di Cantor prende il nome da Georg Cantor, matematico russo-tedesco del XIX secolo che trasformò radicalmente la concezione matematica dell’infinito, degli insiemi infiniti.
La polvere di Cantor si ottiene con il seguente procedimento:
Passo 0 : si parte da un segmento di lunghezza l (nell’immagine è stato aggiunto uno spessore per maggiore chiarezza).
Passo 1 : si divide il segmento in 3 parti uguali e si elimina la parte centrale.
Passo 2 : ogni segmento così ottenuto lo si divide ancora in 3 parti e si elimina la parte centrale.
Ripetendo tale procedimento si ottiene un oggetto frattale di dimensione
D=logN /log(1/r)= log2/log3 = 0.63 (N= 2 r =1/3)
e lunghezza che tende a 0
L0 = l L1 = l·2/3 L2 =l·(2/3)2 …. Ln = l·(2/3)n lim Ln = 0
n ->∞
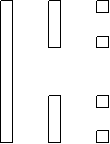
Ripetendo il procedimento all’infinito si ottiene una polvere di
punti che Mandelbrot definisce cagliata frattale, perché ricorda
il modo in cui nel latte i grumi di caglio si separano dal siero.
Triangolo di Sierpinski
Waclaw Sierpinski, matematico polacco del secolo scorso si imbatté in questa forma particolare forse osservando alcuni disegni ornamentali.
Il frattale che prende il suo nome e che Mandelbrot chiama gerla di Sierpinski, nasce da un triangolo equilatero di lato l (passo 0), si suddivide il triangolo equilatero in 4 triangoli equilateri di lato l/2 e si elimina il triangolo centrale (passo 1), si ripete l’operazione per ogni triangolo così formato (passo 2).Si ottiene così un oggetto frattale molto frastagliato e traforato come un merletto.
La dimensione del triangolo di Sierpinski è D = log N / log(1/r) = log 3/log 2 =1.58



passo 0 passo 1 passo 2
Il più famoso frattale : l’insieme di Mandelbrot (fig.2)
Il procedimento utilizzato da Mandelbrot è molto semplice ed è basato su la rappresentazione grafica di una formula ricorsiva molto semplice:
Xn+1 = Xn2 + c
con c numero complesso c= re +i im
re = parte reale di c im = coefficiente dell’immaginario di c
con –2,25 < re < 0,75 e -1,5 < im < 1,5
Xn indica il valore di X al passo n , Xn+1 indica il valore di X al passo successivo.
La possibilità di Mandelbrot di utilizzare i computer e la computer graphic ha permesso di realizzare immagini bellissime e di sottolinearne i dettagli riscoprendo il essi l’insieme di Mandelbrot di partenza (fig.3).
I frattali e l’informatica
Parte del successo della geometria dei frattali si deve imputare alla possibilità di ricreare facilmente al computer immagini frattali.
Le regole di costruzioni degli oggetti frattali sono basate sulla ricorsività, che rende molto facile la realizzazione grafica di tali oggetti.
Chiariamo il concetto di ricorsività con un esempio.
In matematica n! , ossia il fattoriale di n, indica il prodotto di tutti gli interi da 1 fino a n quindi n! = 1 · 2 · 3 · · · n
Si vede facilmente che n! = (n-1)!· n
Questa è una funzione ricorsiva, ossia una funzione che richiama se stessa nella definizione, infatti per calcolare il fattoriale di n basta saper il fattoriale di n-1 e moltiplicare il risultato per n.
Il computer elabora facilmente funzioni ricorsive: basta sapere il punto di partenza, nel nostro caso il fattoriale di 1 che vale 1, ossia 1! = 1 e quindi
2! = 1! · 2 =1 · 2= 2 3! = 2! · 3 = 6 4! = 3! · 4 = 6 · 4 = 24 ecc
Vediamo il listato del programma in Turbo Pascal per la costruzione della curva di Koch in cui la procedura fioccodineve contiene in sé la procedura lato che è ricorsiva.
Se il passo è 0 la procedura lato disegna un segmento
![]() altrimenti
divide il lato per 3, riduce il passo di 1 e
altrimenti
divide il lato per 3, riduce il passo di 1 e
disegna la spezzata (se il passo è 0 ) richiamando 4 volte
la procedura lato , altrimenti richiama
la procedura lato che ricorsivamente ripete il procedimento fino a quando il passo non diventa 0.
La procedura fioccodineve disegna un triangolo (se il passo è 0) altrimenti disegna la stella di Davide (se il passo è 1) o la curva di Koch al passo 2 ecc…
Il programma è strutturato in modo da poter stabilire la lunghezza del lato iniziale e il passo della curva di Koch e usa la grafica della tartaruga( turtle graphic) ossia un triangolino colorato che lascia una scia al suo passaggio ( istruzione forwd(l) ), può ruotare a destra o a sinistra di un determinato angolo (istruzione turnright(60), turnleft(120) ) e posizionarsi sul piano cartesiano ( setposition( -50,-80) ).
Programma in Turbo Pascal sulla costruzione della curva di Koch
Program frattali;
{$i graph.p}
var l,passo:integer;
procedure fioccodineve(l,passo:integer);
var i:integer;
procedure lato(l,passo:integer);
begin
if passo=0 then forwd(l)
else begin
passo:=passo-1;
l:=l div 3;
lato(l,passo);
turnleft(60);
lato(l,passo);
turnright(120);
lato(l,passo);
turnleft(60);
lato(l,passo);
end;
end;
begin
for i:=1 to 3 do
begin
lato(l,passo);
turnright(120);
end;
end;
begin
graphcolormode;
showturtle;
write('inserisci la lunghezza del lato ');
readln(l);
write('inserisci il passo');
readln(passo);
setposition(-50,-80);
fioccodineve(l,passo);
hideturtle;
end.
La geometria del cavolo
Le nuvole non sono sfere, le montagne non sono coni, le coste non sono cerchi e la corteccia degli alberi non è liscia, né il fulmine viaggia in linea retta.
Benoît Mandelbrot
Il titolo è provocatorio, ma non molto lontano dal vero: infatti uno dei primi esempi di oggetto frattale in natura, utilizzato dallo stesso Mandelbrot per chiarire meglio la proprietà dell’autosomiglianza, è proprio il cavolo anzi il cavolfiore.
Ogni cimetta del cavolfiore è un piccolo cavolo essa stessa e staccata dal cavolo grande e disposta su di un ripiano senza elementi di confronto non permette di individuare chi è il cavolo e chi la cimetta.
Ma la natura ha spessissimo strutture frattali: le foglie degli alberi, le felci (fig.4) hanno strutture frattali perfettamente riconoscibili, ma ogni albero si basa su regole di ramificazioni elementari e ricorsive ( un tratto lineare ed una ramificazione, e poi ancora un tratto più sottile lineare ed un’altra ramificazione su ogni ramo ecc…).
La linfa nelle piante e nelle foglie segue percorsi frattali. Le spugne marine, i coralli hanno processi frattali di accrescimento.
Nel corpo umano la circolazione del sangue, i bronchi , i polmoni hanno strutture frattali (fig.5).
I biologi Jim Brown e Brian Enquist e il fisico Geoffrey West hanno dimostrato che il sistema circolatorio dei mammiferi e quello delle radici e dei rami degli alberi sono delle strutture frattali, ne hanno calcolato la dimensione fratta che è risultata la stessa per entrambi i sistemi.
Le nuvole, i vortici caotici, i fulmini sono frattali che possono essere riprodotti al computer.
Tutte le coste o i rilievi montuosi sono formati da avvallamenti e sporgenze che si ripropongono secondo modalità frattali.
Le coste italiane
Mandelbrot nel suo libro Gli oggetti frattali si pone il problema di calcolare la lunghezza delle coste della Bretagna. Noi possiamo partire dalle coste italiane utilizzando il suo ragionamento: prendiamo una cartina dell’Italia e con un segmento corrispondente a 100 km (nella scala della cartina geografica) ricopriamo la costa italiana. Ne disegneremo circa 50. Quindi la lunghezza delle coste italiane in prima approssimazione è 50 X 100 = 5000 km.
Prendiamo ora una cartina stradale ed utilizziamo un segmento corrispondente a 1 km: ne occorreranno 6000 per ricoprire tutta la costa italiana, quindi la lunghezza della costa italiana è di 6000 km. Alla scala di 1 m la lunghezza della costa italiana diventerebbe 10000 km. E riducendo ancora la scala otterremmo una lunghezza sempre maggiore. Quindi osserviamo che scale diverse portano a calcolare lunghezze molto diverse! E che estremizzando questo ragionamento si arriva a dire che le coste italiane (ma anche britanniche come dice Mandelbrot nel suo trattato) e quindi le coste di tutte le nazioni hanno una lunghezza che tende all’infinito!
Questo risultato paradossale deve farci capire che il profilo di una qualunque costa è un oggetto frattale la cui lunghezza può essere calcolata solo fermandosi ad un determinato passo di precisione. Nel caso delle coste italiane con una scala adeguata (in grado di considerare le irregolarità più significative ma senza perdersi in dettagli insignificanti) si può considerare il valore di 8000 km come corretto.
I frattali in arte
L’architettura di molte chiese in varie epoche ha una struttura frattale. Esempi famosi sono le cattedrali gotiche in cui strutture elementari si ripetono a diverse scale ritrovando la proprietà frattale dell’autosomiglianza. Lo stesso Mandelbrot ha citato l’esempio dell’Opera di Parigi come di un edificio dotato di simmetria di scala. Camminando lungo la Rue de l’Opera, più ci si avvicina più si notano i dettagli autosimili dell’edificio.
La ricorsività è poi un elemento costante di tutta la produzione di Escher .Nella litografia « Mani che disegnano » (fig.6) la mano destra disegna la mano sinistra che disegna la mano destra ecc… in un ciclo infinito e surreale.
Nella litografia « Mano con sfera riflettente » (fig.7) la mano di Escher sostiene una sfera che riflette l’immagine di Escher che sostiene una sfera che riflette l’immagine di Escher ecc.. ancora una rappresentazione per immagini della ricorsività.
I frattali nelle scienze sociali
Alcuni insediamenti abitativi di popolazioni nel sud dello Zambia (Baili) mostrano una distribuzione frattale: Si tratta di un grande recinto per il bestiame formato da abitazioni disposte ad anello. Più grande è l’abitazione, più importante è la famiglia, fino ad arrivare alla casa del capo, posta al centro. Al centro di ogni abitazione è posto l’altare domestico circondato da un piccolo recinto secondo una gerarchia frattale(fig.8).
I frattali in economia
Nel 1900 un giovane matematico francese, Luis Bachelier, studiò i mercati finanziari sviluppando un modello per cui i prezzi di un’azione o di un titolo non sono prevedibili ma le loro oscillazioni possono essere descritte dalle leggi matematiche del caso. Il rischio quindi è misurabile e controllabile. Il punto focale è che i prezzi scendono o salgono con pari probabilità (come per il lancio di una moneta: la probabilità che esca testa o croce è sempre ½) e che la variazione dei prezzi è misurabile. Per il 68% le variazioni oscillano intorno alla media di una quantità inferiore alla deviazione standard, che è un indice statistico che misura da dispersione dei dati, nel 95% dei casi lo spostamento è inferiore a 2 deviazioni standard, nel 98% inferiore a 3 deviazioni standard. Il grafico delle variazioni del prezzo di un titolo risulta una curva a campana, detta normale o gaussiana (fig.9)dal nome del grande matematico tedesco Carl Friedrich Gauss, le numerose piccole variazioni si addensano intorno alla media al centro della campana, le rare variazioni grandi ai margini.
Ogni evento casuale, le altezze di una popolazione, i risultati di un compito in classe, sottostanno ad una distribuzione gaussiana. Una teoria molto elegante, accettata in campo finanziario da tutti gli economisti fino ad oggi, ma che, anche se solo nel campo finanziario, è risultata errata come dimostrano gli andamenti schizofrenici dei prezzi della Borsa degli anni Novanta. I due punti fondamentali del modello di Bachelier sono l’indipendenza statistica delle variazioni dei prezzi e la loro distribuzione normale. Mentre la realtà non è così : le variazioni dei prezzi non sono indipendenti, quello che accade oggi influenza quello che accadrà domani, e non seguono affatto la curva a campana. Lo denunciano i movimenti del Dow Jones dal 1916 al 2003 (fig.10) : i giorni con variazioni superiori al 3,4% dovevano essere 58: sono stati 1001. I giorni con oscillazioni superiori al 4,5% dovevano essere 6: sono stati 366. Oscillazioni superiori al 7% dovevano verificarsi ogni 300000 anni:si sono verificate 48 volte. Questo dimostra che il modello utilizzato non è idoneo.
![]() Mandelbrot
ha studiato un modello frattale per lo studio dell’andamento finanziario dei
prezzi in Borsa.
Mandelbrot
ha studiato un modello frattale per lo studio dell’andamento finanziario dei
prezzi in Borsa.
Si parte da un segmento ascendente se si vuole descrivere
![]() un
andamento positivo (discendente se negativo).
un
andamento positivo (discendente se negativo).
Si sostituisce il segmento di partenza con una spezzata,
che rappresenta il generatore del grafico frattale.
Al passo successivo ogni segmento della spezzata viene sostituito con la stessa spezzata rimpicciolita. Si costruisce così un grafico frattale sempre più frastagliato ad ogni passo. Con questo metodo si può costruire un modello matematico frattale che può imitare la variazione di un prezzo di un prodotto: non seguirà il cammino reale ma si comporterà statisticamente nelle stesso modo. Sembra che questi modelli frattali siano uno strumento più valido per lo studio delle variazioni dei prezzi nel mercato azionario e in campo finanziario in genere.
Caos e frattali
Le stelle e le galassie in moto nel cielo costituiscono un sistema dinamico che è stato studiato per secoli da migliaia di scienziati; il mercato azionario è un altro sistema dinamico che varia nel tempo, così come le condizioni meteorologiche sulla Terra. L’aumento o la diminuzione di una popolazione o anche il moto di un pendolo sono sistemi dinamici. Per alcuni di essi è possibile prevederne l’evoluzione, per altri non è altrettanto semplice a causa delle troppe variabili che interagiscono: è possibile prevedere il moto dei pianeti ma non le variazioni atmosferiche a lungo termine o l’indice Dow Jones con una settimana di anticipo. Ma anche sistemi dinamici con una sola variabile possono comportarsi in maniera altrettanto caotica. Modelli generati da funzioni quadratiche iterate portano allo studio del caos e la geometria dei frattali aiuta a dare di tali fenomeni una rappresentazione grafica. Il caos ci circonda : un uragano, un torrente in piena, le volute di fumo, il mercato finanziario hanno tutti un comportamento caotico, ma oggi con i frattali si apre uno spiraglio verso la comprensione e la previsione di tali fenomeni.
I frattali nel liceo Vittorio Emanuele II
Nell’anno scolastico 1991/92 gli alunni della III A hanno realizzato una pubblicazione sulla geometria dei frattali, implementando programmi in Turbo Pascal per la costruzione di oggetti frattali, approfondendo lo studio della dimensione frazionaria di alcuni frattali, e raccogliendo immagini dei più famosi frattali.
Durante il Vittorio Emanuele Day 2002 nel laboratorio di Informatica si è tenuta una mostra sulla geometria dei frattali con una sezione dedicata ai Frattali in natura, (fig.11), una galleria di Frattali inserita in rete nel sito del liceo Vittorio Emanuele II ( www.liceovittorioemanuele.it/frattali/frattali.htm) ed attività di laboratorio con la costruzione di programmi in Turbo Pascal per la realizzazione di oggetti frattali, da parte degli allievi del corso liceale sez. A che hanno partecipato al progetto durante tutto l'anno scolastico 2001/2002.
Spesso i frattali sono entrati nel programma di matematica e informatica del corso liceale sez. A per abituare gli alunni a ragionare in termini più ampi, avvicinandoli al concetto di geometria, che non è solo quella euclidea, di dimensione, che non è solo intera, di ricorsività, fondamentale in informatica, alla base di tutte le costruzioni dei frattali.
Avvicinarsi alla geometria dei frattali può aiutare anche i non addetti ai lavori a conoscere meglio la realtà che ci circonda e scoprire che in fondo la natura utilizza semplici regole per la costruzione di tutti i più complessi sistemi : semplicità e complessità : un’antitesi felicemente superata.
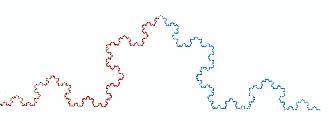
Fig.1 Un lato della curva di Koch
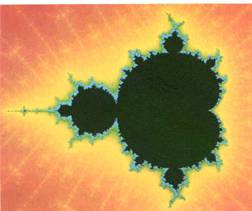

Fig.2 Insieme di Mandelbrot Fig.3 Dettaglio dell’insieme di Mandelbrot

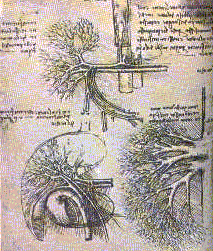
Fig.4 Felce al computer Fig.5 Leonardo da Vinci . Corpo umano


Fig.6 Mani che disegnano Fig.7 Mano con sfera riflettente
M.C.Escher - Litografia M.C. Escher -Litografia –1935

Fig.8 Frattali nella società.
Veduta aerea degli insediamenti di Ba-ili nel sud dello Zambia
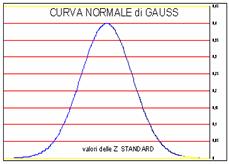
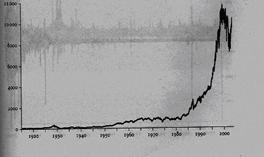
Fig. 9 Curva Normale di Gauss Fig.10 L’indice Dow Jones dal 1916 al 2002

Fig.11 Frattali in natura
Mostra al LiceoVittorio Emanuele II – giugno2002
Bibliografia
Benoît B.Mandelbrot, Gli oggetti frattali. Forma , caos e dimensione,Einaudi , 1987
Benoît B.Mandelbrot, Richard L. Hudson, Il disordine dei mercati, Einaudi, 2005
Robert L.Devaney, Caos e frattali. Matematica dei sistemi dinamici e applicazioni al
calcolatore,Addison-Wesley, 1990
Heinz-Otto Peitgen, Peter H.Richter, La bellezza die frattali. Immagini di sistemi
dinamici complessi,Bollati Boringhieri,1987
John Briggs, L’estetica del Caos. Avventure nel mondo dei frattali: scienza, arte e natura, Red Edizioni,1993
F.Rossati, G.Gamarino, Frattali, Levrotto & Bella Torino,1991
M.C.Escher, Grafica e disegni,Benedikt Taschen,1992
Nicola Fusco, I frattali: una teoria geometrica della complessità in «Come alla Corte dei Federico II ovvero parlando e riparlando di scienza»,Università degli Studi di Napoli Federico II, I quaderni di Coinor, 2003
Oriana Pagliarone, Una lezione particolare: la geometria dei frattali in «Il tempo della scuola» anno II - ottobre 1992, Morano Editore