

Frattale costruito partendo da un esagono regolare
fib(n+1)/fib(n)
√n
4 9 2
3 5 7
8 1 6
![]()
![]()
![]()
![]()
![]()
1 1 2 3 5 8 ...
fibo(1)=1 , fibo(2)=1
fibo(n)=fibo(n-1)+fibo(n-2) per n >2
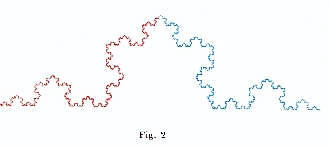
Programma che disegna la Curva di Koch

[-1,2,2,3]
Il computer sceglie un numero intero positivo<100 in modo casuale , il giocatore deve scrivere s se il numero Ŕ multiplo di 7 o inizia o termina per 7 , n in caso contrario .Il programma Ŕ completato da ritornelli (inno alla gioia , la pantera rosa ecc..) a seconda delle risposte: le procedure dei ritornelli sono realizzate calcolando le frequenze delle note e utilizzando le istruzioni sound, nosound e delay.
(Il programma utilizza gli array per descrivere ogni labirinto)

a21 a22 a23
a31 a32 a33

Il programma, di cui ho scelto la versione di un mio ex alunno , Fulvio Scia (a.s.88/89), disegna vari alberi di Natale, con la grafica del Turbo Pascal, con accompagnamento musicale(Jngle Bells) (costruito nota per nota mediante procedure realizzate calcolando le frequenze delle note e utilizzando le istruzioni sound, nosound e delay).
1 3 6 10 15 ....
tri(n)=1+2+3+....n
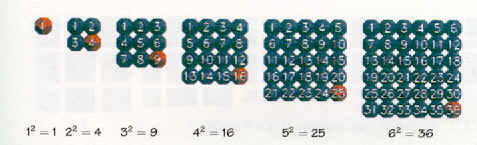
q(n)=1+3+5+7+ ...+2n-1=n2

1+4+7+10+...+
1 5 12 22 ....

1+5+9+13+...+
1 6 15 28...

(numeri piramidali a base triangolare)
1+3+6+10+...+
1 4 10 20....

1 + 4 + 9 + 16+... +
1 5 14 30
| 0 | 2 | 3 | 0 | 5 | 0 | 7 | 0 | 0 | 0 |
| 11 | 0 | 13 | 0 | 0 | 0 | 17 | 0 | 19 | 0 |
| 0 | 0 | 23 | 0 | 0 | 0 | 0 | 0 | 29 | 0 |
| 31 | 0 | 0 | 0 | 0 | 0 | 37 | 0 | 0 | 0 |
| 41 | 0 | 43 | 0 | 0 | 0 | 47 | 0 | 0 | 0 |
| 0 | 0 | 53 | 0 | 0 | 0 | 0 | 0 | 59 | 0 |
| 61 | 0 | 0 | 0 | 0 | 0 | 67 | 0 | 0 | 0 |
| 71 | 0 | 73 | 0 | 0 | 0 | 0 | 0 | 79 | 0 |
| 0 | 0 | 83 | 0 | 0 | 0 | 0 | 0 | 89 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 97 | 0 | 0 | 0 |
per l'individuazione dei numeri primi
1 1 1 2 2 3 4 ....
pado(n)=1 per n=1,2,3
pado(n)=pado(n-2)+pado(n-3) per n >3
p
pado(n+1)/pado(n)
D
izionario etimologico di 27 parole in dialetto napoletano derivanti dal greco e 23 dal latino, con la traduzione in polacco per il gemellaggio del Liceo Vittorio Emanuele II con il Liceo Novodowskiego di Cracovia a.s.1989/90 (ho scelto la versione di Fulvio Scia ed Antonio Ciccarelli)Il programma realizza anche il disegno delle bandiere italiana e polacca, del golfo di Napoli e un karaoke antelitteram dell'inno italiano e di quello polacco.
Questo programma consente di calcolare i primi k numeri primi (k<=10000),
di individuare se un numero p Ŕ primo (1<p<10000) e di calcolare la
scomposizione in fattori primi di un numero m
1 1/3 1/6 1/10 1/15 .....

Frattale costruito partendo da un segmento che si ramifica
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 2 3 4 5 6 ...
1 3 6 10 15 ...
1 4 10 20 ...
1 5 15 ...
1 6 ...
1 ...
ai,j=
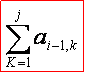
1 2 3 4 5 6 ...
1 3 6 10 15 ...
1 4 10 20 ...
1 5 15 ...
1 6 ...
1 ...
ai,j = a i-1,j + ai,j-1
1/1 1/2 1/3 1/4 1/5 ...
1/2 1/6 1/12 1/20 ....
1/3 1/12 1/30 ...
1/4 1/20 ...
1/5 ...
armoi,j = armoi-1,j- armoi-1,j+1
1/2 1/6 1/12 1/20 ....
1/3 1/12 1/30 ...
1/4 1/20 ...
1/5 ...
Questo programma verifica che la serie della prima riga del triangolo armonico diverge all'infinito, mentre le serie di ogni riga i-esima convergono ad armo(i-1,1)
 ,
,